5.4.3. Quadrature encoder support¶
5.4.3.1. Overview¶
MCAF supports the use of a quadrature encoder (with or without index pulse) for closed-loop velocity operation, through the dsPIC® DSC QEI (Quadrature Encoder Interface) peripheral.
Use of a quadrature encoder can be very valuable during prototyping stages, and it can be used in conjunction with a sensorless estimator to validate or troubleshoot estimator operation. MCAF allows more than one estimator to execute — at the cost of additional CPU usage — but only one estimator can be used for commutation.
A quadrature encoder can provide accurate tracking of relative position changes, as long as the encoder signals are received without significant errors. Furthermore, angle resolution is a function of the encoder; high-end encoders can provide thousands of counts per mechanical revolution. An encoder cannot, however, provide these features on its own:
absolute position accuracy at all times
Encoders without index pulses can never provide absolute position accuracy
Encoders with an index pulse can provide absolute accuracy once the index pulse has been detected, but prior to that, there is no way to determine absolute position from the encoder
a measurement of velocity — the encoder provides quantized position; velocity must be estimated from position through a separate algorithm
determination of the electrical commutation offset for a PMSM, to locate the motor’s position of maximum rotor flux relative to encoder position
MCAF provides these features with back-emf synchronization for determining commutation offset, and a tracking loop for estimating velocity from position.
5.4.3.1.1. Usage notes¶
Encoders are usually specified in “lines” or “cycles per revolution” (CPR). There is a 4:1 relationship between counts per revolution and lines or CPR: for example, 256 lines = 256 CPR = 1024 counts per revolution.
The dsPICDEM® MCLV‑2 Development Board has 100 pF filter capacitors on its encoder/Hall inputs. These may cause problems for encoders with high count rates, in which case capacitors C49, C50, and C51 should be removed, or replaced with smaller values such as 10 pF.
5.4.3.1.2. Limitations¶
As of MCAF R7:
Position control is not supported
Operation near zero speed is not supported — the QEI support is limited to use as a drop-in replacement for sensorless estimators, and startup through forced commutation is required.
Index pulses are supported only for encoder resolutions that are a power of two. Non-power-of-two encoder counts are supported by the QEI peripheral’s modulo mode; index pulses are supported by the use of the QEI peripheral’s position capture feature, which cannot be used simultaneously with modulo mode in dsPIC® DSC 33F, 33E, and 33C devices.
5.4.3.2. Tracking loop¶
5.4.3.2.1. Overview¶
There are many ways to estimate velocity from encoder position. A naïve implementation would attempt to differentiate the velocity signal, but because the encoder quantizes rotor position, the result at moderate speeds would be a bunch of zeros and ones. (For example, consider a 1024 count-per-revolution encoder on a motor running at 1000 RPM = 16.667 revolutions/second. This produces encoder counts at the rate of around 17067 counts/second. A control ISR running at 20 kHz would see a change of either 0 or 1 counts per ISR. At 10000 RPM the same motor/encoder pair would produce 170667 counts/second, and the control ISR would see either changes of either 8 or 9 counts per ISR. In either case, the maximum quantization error of velocity would equal 0.5 counts per ISR = 1/2048 revolution * 20 kHz = 9.77 revolutions/second = 586 RPM.)
One way to estimate velocity is to compute the change in position each control cycle, and use a low-pass filter to determine velocity. MCAF uses something slightly different, known as a tracking loop.
Tracking loops are essentially just a low-pass filter in state-variable form to produce useful estimates. In the tracking loop shown in Figure 5.56, the input angle \(\theta\) may be noisy, whether through analog noise or, in the case of an encoder, quantization noise. The loop itself just consists of a PI controller to estimate a velocity \(\hat{\omega}\) which is then integrated to form an estimated angle \(\hat{\theta}\) used to form an error term for the PI loop.
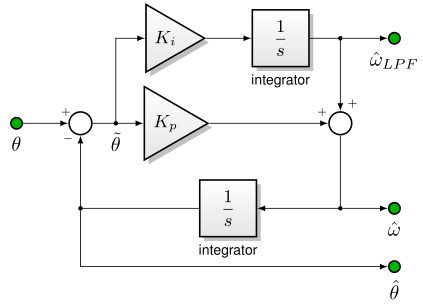
Figure 5.56 Tracking loop for estimating velocity from position¶
The outputs of a tracking loop are
\(\hat\omega_{LPF}\) — the integrator output can be used as a moderate-bandwidth estimate of velocity.
\(\hat\omega\) — the PI output contains high-frequency content needed to drive the error towards zero. It is generally not appropriate for general use, because noise from \(\theta\) feeds directly into it from the proportional (P) term.
\(\hat\theta\) — the estimated angle filters out high-frequency component of quantization noise, and can be used for position control applications; it can also be used for commutation applications, but the phase lag is critical and must be analyzed carefully.
Note on the choice of units: a tracking loop can operate equally well on any sort of quantity that requires estimation of a low-frequency derivative; its input could be temperature in °C, with an output in °C/s, rather than an input of position with an output of velocity.
5.4.3.2.2. Frequency-domain equivalent¶
Transfer functions from real angle/velocity inputs (assuming additive noise) to outputs are:
A few things to note:
The denominator in all cases forms a 2nd-order system, and can be written in the form \(\tau^2s^2 + 2\zeta\tau s+1\) with \(K_i = 1/\tau^2\) and \(K_p = 2\zeta/\tau\). The quantity \(\zeta\) represents damping factor and should be set conservatively, perhaps something in the 1 – 1.5 range. The time constant \(\tau = 1/\omega_n\) is inversely proportional to bandwidth.
The velocity transfer function to \(\hat{\omega}_{LPF}\) has no zeros; the velocity transfer function to \(\hat{\omega}\) has a zero at \(s=-K_i/K_p=-1/2\zeta\tau\).
5.4.3.2.3. Implementation Notes¶
The tracking loop used in MCAF for quadrature encoder support operates on mechanical angle \(\theta_m\), with an output of estimated mechanical angular velocity \(\omega_m\). This choice preserves angular location within one complete mechanical rotation, to support future position control applications.
MCAF uses the filtered velocity, \(\hat{\omega}_{LPF}\), for velocity estimates.
The MCAF implementation of the tracking loop adds a limiter block, shown in Figure 5.57, which prevents overflow in the calculation of \(\hat\omega\).
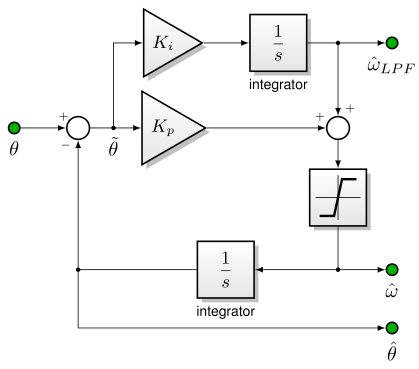
Figure 5.57 Tracking loop implementation¶
5.4.3.3. Back-EMF synchronization¶
The goal of back-EMF synchronization is to estimate a commutation offset such that FOC can operate with a reference frame in perfect alignment. When a rotor (\(dq\)) reference frame is perfectly aligned with a PMSM’s rotor flux and back-EMF, it has the following properties:
back-EMF — With \(I_q = I_d = 0\) at nonzero speed, the terminal voltage of the motor is along the q-axis and is proportional to mechanical velocity \(\omega_m\); the terminal voltage has no d-axis component. Changes in commutation offset would cause nonzero d-axis component.
d-axis torque — With \(I_q = 0, I_d \ne 0\), no torque is produced. Small changes in commutation offset would cause a net electromechanical torque that is proportional to \(\tilde\theta\), the error in commutation offset: \(T_{em} = \frac{3}{2}K_eI_d \sin\tilde\theta\).
q-axis torque direction — With \(I_d = 0, I_q > 0\), positive torque is produced. (180° offset error produces negative torque)
MTPA — For surface permanent magnet motors (SPMSM), \(I_d = 0, I_q > 0\) produces maximum torque, and any change in commutation offset reduces the generated torque. This condition is known as “maximum torque per ampere” or MTPA.
anisotropy due to saturation — With \(I_q = 0, I_d > 0\), iron saturation occurs at a lower current than with any change in commutation offset. Saturation results in a decreased incremental inductance \(\partial \psi \over \partial I\). This is because the stator field adds to the magnetic field of the rotor to maximize the resulting stator field for a given stator current.
anisotropy due to saliency — For motors with rotor saliency (such as interior permanent magnet motors = IPMSM), the d- and q-axes are eigenvectors of the inductance matrix, and therefore changes in \(I_d\) produce changes in stator flux \(\psi_d\) with no change in \(\psi_q\), and similarly changes in \(I_q\) produce changes in stator flux \(\psi_q\) with no change in \(\psi_d\). In other words, the flux equation can be written in the form shown in equation 5.27, which has no off-diagonal terms in the inductance matrix. Changes in commutation offset would cause nonzero cross-axis terms in the flux equation.
All sensorless estimators take advantage of at least one of these properties to discern the true rotor reference frame, with various tradeoffs in bandwidth, stability, convergence, complexity, power consumption, and accuracy.
MCAF R4 introduced back-emf synchronization in the qei_sync module. One of three methods
can be selected, each of which interacts with hooks in the startup sequence:
align — the align method applies a fixed current at a fixed angle during the align phase of startup, and expects that the rotor has a minimal mechanical load at low speeds and will rotate so that its d-axis aligns with the applied current vector. (This method relies on the d-axis torque property.) This is the default method of MCAF, is very fast, and works well for most motors, as long as cogging torque or other mechanical loads are relatively low, and the effect of any rotor saliency is fairly small at low torque loads.
pullout — the pullout method reduces the current used in the spin phase of startup until it observes the rotor angle start to decrease significantly from the angle of applied current. (This method relies on the MTPA property.) This method is immune from errors in cogging torque, but is sensitive to the dynamics of forced commutation.
align-and-sweep — the align-and-sweep method applies a fixed current at a slowly changing angle during the align phase of startup. The applied electrical angle rotates through one full mechanical rotation in both forward and reverse directions, and over the two resulting intervals, averages the difference between applied electrical angle and measured encoder angle to obtain an estimate of commutation offset. This method is slow but can produce very accurate estimates of commutation offsets in most motors.
These methods are described in more detail in the following sections.
In all cases, commutation offset is estimated during only one startup iteration; once complete, the resulting value is reused, and subsequent startup sequences will skip back-emf synchronization.
