5.5.2. Maximum Torque Per Ampere (MTPA)¶
5.5.2.1. Overview¶
For a surface PMSM, \(I_{d} = 0\), \(I_{q} > 0\) results in Maximum Torque Per Ampere (MTPA) operation of the motor. In a PMSM with salient pole rotor (e.g. Interior PMSM or IPMSM), the d and q axis inductance values are different and often \(L_{q} > L_{d}\). For a salient-pole motor, the torque equation is given by 5.52. The electromagnetic torque produced here is contributed by two terms. The first term is the permanent magnet torque and the second term is the reluctance torque. The reluctance torque is produced in the motor as a result of saliency.
Since \(L_{q} > L_{d}\), the reluctance torque can be made to aid the permanent magnet torque if \(I_{d} < 0\). With a suitable negative \(I_{d}\) value, the motor can be operated at the maximum efficiency yielding Maximum Torque Per Ampere (MTPA) in an IPMSM. The aim of the MTPA algorithm is to calculate such a d-axis current reference (\(I_{d\_mtpa}\)) for a given operating point of the motor.
5.5.2.2. Flow chart and description¶
The value of \(I_{d}\) at which the motor operates at maximum efficiency thereby yielding MTPA is derived from the torque equation, and is given by 5.53. Here, \(\Psi_{\mathrm{PM}}\) is the back emf constant in volts per electrical rad/s units and \(L_{1}\) is the differential inductance given by \(L_{1} = \frac{L_d - L_q}{2}\). In addition to the motor parameters \(\Psi_{\mathrm{PM}}\) and \(L_{1}\), the d-axis current needed to ensure MTPA (\(I_{d\_mtpa}\)) is a function of the q-axis current \(I_{q}\).
Figure 5.85 shows the flow chart of the MTPA algorithm.
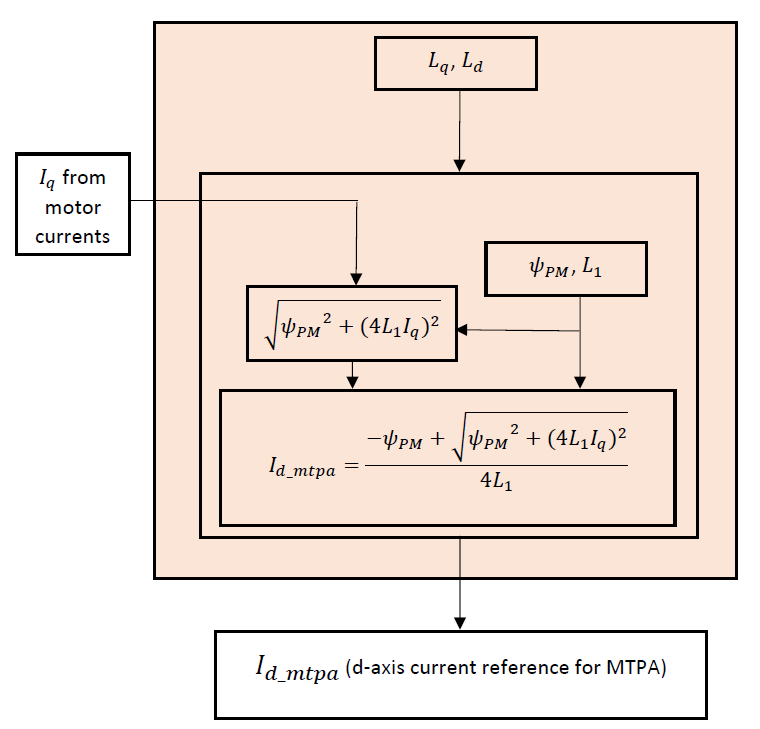
Figure 5.85 MTPA algorithm flow chart¶
\(I_{d\_mtpa}\) value is calculated using 5.53. This calculated value further goes to D-axis current reference generation and is used to generate \(I_{d\_ref}\).
5.5.2.3. Implementation notes¶
Added in R6.
Low-saliency optimization: In case the motor saliency is low (\(L_d \approx L_q\)), the MTPA calculation is skipped to reduce CPU usage, and \(I_{d\_mtpa}\) is set to zero. This is done if the saliency ratio \(\xi = \frac{L_q}{L_d}\) is less than a user-defined saliency threshold.
Square-root calculation: The present MTPA algorithm uses a full machine-precision square-root calculation. To reduce the CPU instruction cycles, the future versions of MCAF may include alternatives to this.
